Multiclass SVM loss:

Given an example $(x_i,y_i)$ where $x_i$ is the image and where $y_i$ is the (integer) label, and using the shorthand for the scores vector: $S=f(x_i,W)$

The SVM loss has the form:

$$\boldsymbol{L}{i}=\sum{j \neq y_{i}} \max \left(0, s_{j}-s_{y_{i}}+1\right)$$

One thing to mention is that SVM let the highest class be a bit much higher than second highest class. So if the highest is too close to the second highest, it also gains loss.

And the full training loss is the mean over all examples in the training data:

$$L=\frac{1}{N} \sum_{i=1}^{N} L_{i}$$

Hinge Loss:

Kind of like SVM.

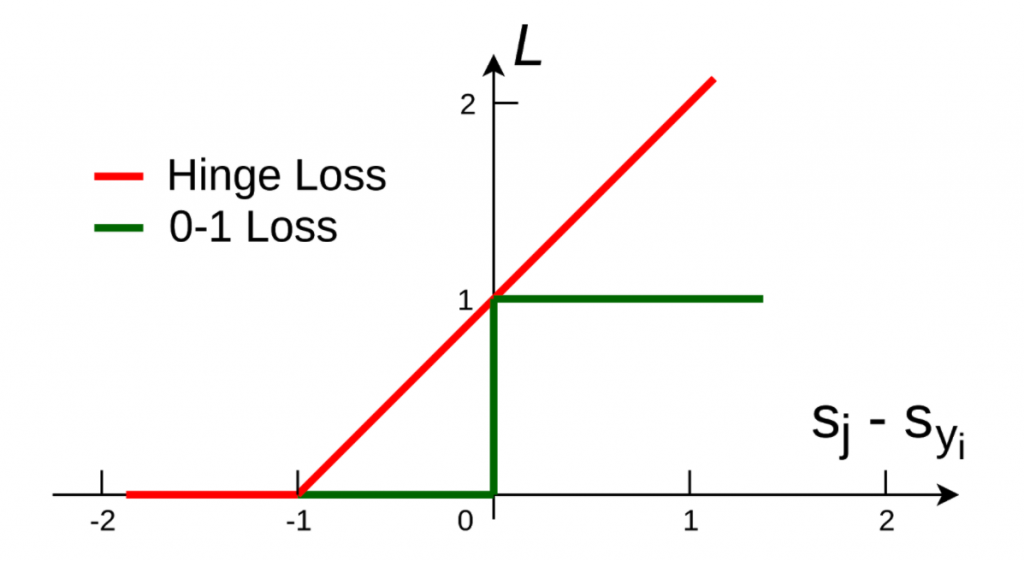
It is better than 0-1 loss because

• it builds in robustness since it builds in a margin of one
• It is differentiable.* — adjust scores to improve things

How could we change W to eliminate the loss?

• By scaling $W$ by a constant does not change its final behavior on any answer, which means the correct always be the correct, it will never change. In other words, it will never switch the position of which class has the biggest score by scaling $W$. We want the score to be relatively bigger.

Regularization

$$L(W)=\frac{1}{N} \sum_{i=1}^{N} L_{i}\left(f\left(x_{i}, W\right), y_{i}\right)+\lambda R(W)$$

Let it not be affected too much by one single feature of the data.

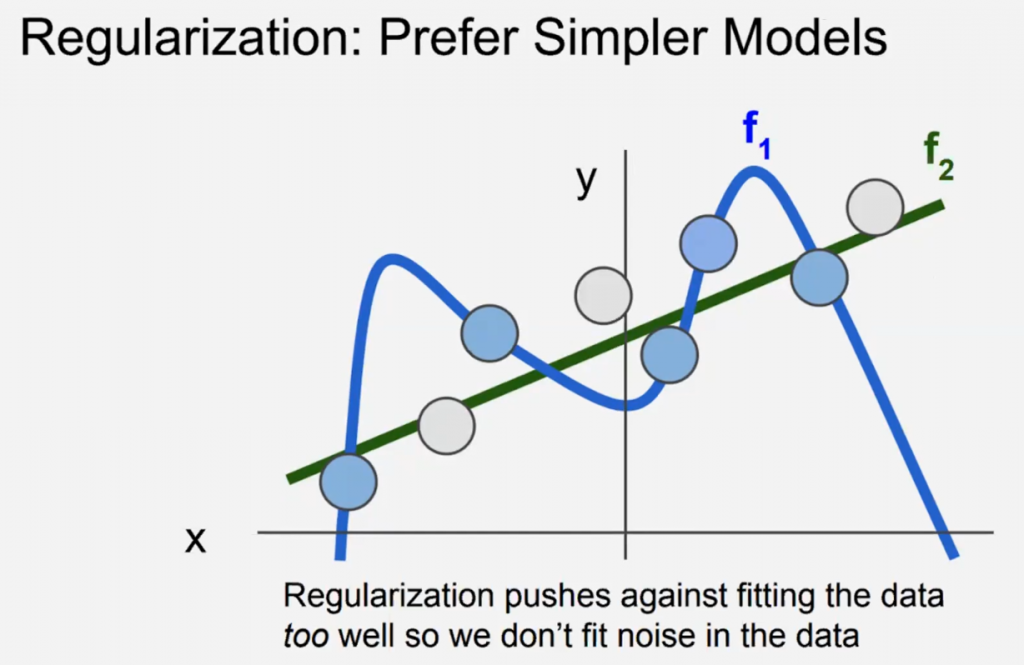
Why not force $W$ to have a FIXED MAGNITUDE?

(1) It makes the optimization process more challenging — it gives you less flexibility in finding the optimum.

Softmax Classifier (Multinomial Logistic Regrassion Loss)

$$L_{i}=-\log \left(\frac{e^{s y_{i}}}{\sum_{j} e^{s_{j}}}\right)$$