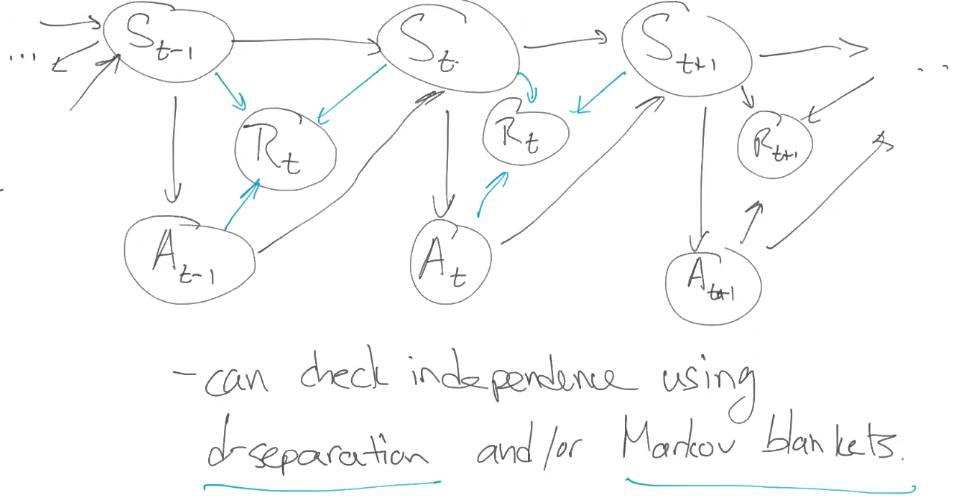
Beyesian Network for an MDP
Agent’s Goal:
To find a policy that maximizes the expected total amount of reward that it will get. (one of many goals in RL literature)
Objective Function
$$J: \Pi \rightarrow \mathbb{R} $$ $J$ is not random. Sometimes $\rho$.
$\Pi$ denotes the set of all policies(uppercase). $$J(\pi)=\mathbb{E}\left[\sum_{t=0}^{\infty} R_{t} \mid \pi\right]$$
Wrong. Will correct it soon!
Since $\Pi$ are policies, not events. So we cannot make it as the conditional expectation.
Reward Discount $\gamma \in [0,1]$
$$J(\pi)=\mathbb{E}\left[\sum_{t=0}^{\infty}\gamma^t R_{t} \mid \pi\right]$$
$\gamma < 1$ means that rewards that occur later are worth less to the agent. One purpose is preventing $J$ from being infinite ($\gamma is not one$:
$$\sum_{i=0}^{\infty} \gamma^{i}=\frac{1}{1-\gamma}$$ Based on this rule, $J$ will be in range $( -\frac{R_{max}}{1-\gamma}, \frac{R_{max}}{1-\gamma} )$
Quests
- Why is this gamma part of the environment MDP, not the agent doing as part of its objective function. — Because it’s part of the problem specification.