Optimization: Stochastic Gradient Descent and Backpropagation 2020-09-12
Hello WorldNeural Networks and aNLP
0 条评论

Recap

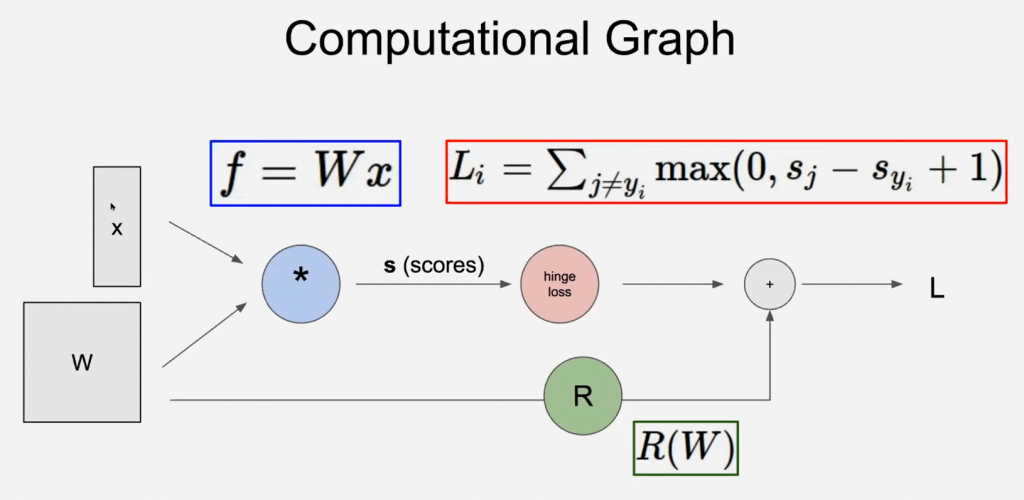
  • We have a score function: $s=f(x ; W) \stackrel{\text { e.g. }}{=} W x$
  • We have a loss function:
    • Softmax: $L_{i}=-\log \left(\frac{e^{e y_{i}}}{\sum_{j} e^{s_{j}}}\right)$
    • SVM: $L_{i}=\sum_{j \neq y_{i}} \max \left(0, s_{j}-s_{y_{i}}+1\right)$
      • Thus, the Full loss $L=\frac{1}{N} \sum_{i=1}^{N} L_{i}+R(W)$

$R(W)–\lambda R(W)$ control the strenth of regularization penalty. 当这个增大的时候会得到一个smoother的boundry, basically by limiting the flexibility of the W matrix. 让W不要太有灵活性，灵活性太高就容易过拟合训练集。训练过程就是捏神经网络形状让它拟合训练数据的过程，就像捏橡皮泥，不能太像训练数据了，会没有泛化能力。控制正则项的梯度反向传播程度。

Gradient descent

  • Numerical gradient: approximate, slow, easy to write
  • Analytic gradient: exact, fast, error-prone

In practice, we always use analytic gradient, but we check implementation with numerical gradient. This is called a gradient check.

Mini-batch Gradient Descent

Only use a small portion of the training set to compute the gradient. (with random subsets)

It just like sampling, since the loss function will give the average loss for data loss.

  • Goal is to estimate the gradient
  • Trade-off between accu and compu
  • No point in doing more computation if it wont change the updates

We take one step according to one sample and update the $W$ once. Then we catch another sample with a constant size of batch, take step, update $W$. Each time we may do harm to some data but in average, the loss is reducing.

Computational Graph