Backpropagation
For instance, if layer 1 is doing: 3.x to generate a hidden output z, and layer 2 is doing: z² to generate the final output, the composed network will be doing (3.x)² = 9.x².
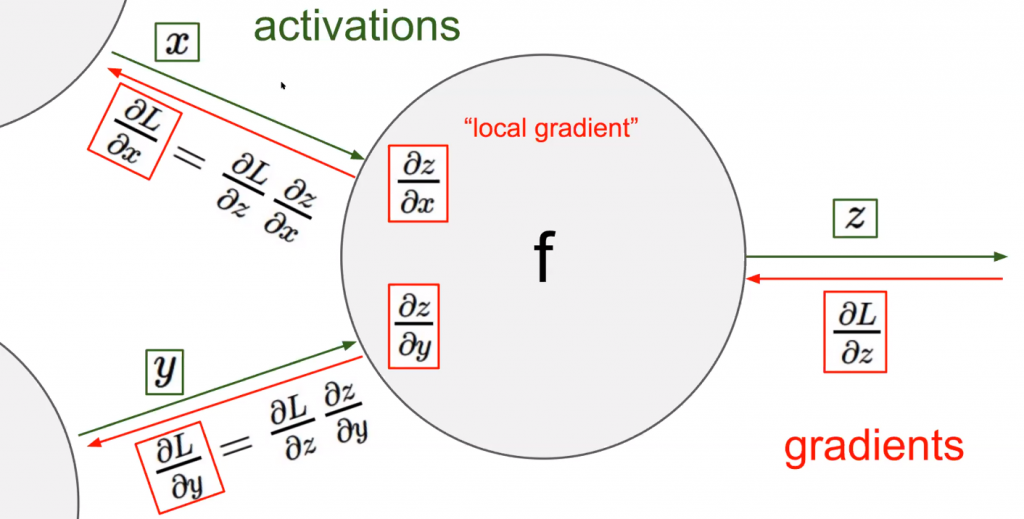
Upstream gradient is the gradient that sends to lower layer. Now we have both local gradient for $f(wx)$ and upstream gradient that contains the global gradient information. It gives to you and you have to combine it with these local gradients and pass it along.
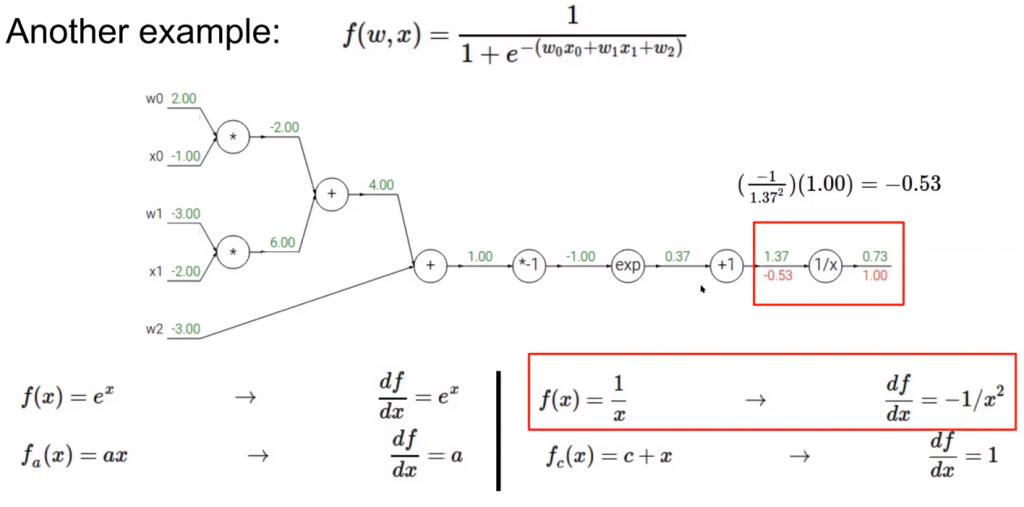
For this example, green stands for the value and red stands for the gradients we calculate. We will update the paramters $w_0,w_1,w_2$ by learning rate formula once we have calculated all the gradients and the backpropagation is over.
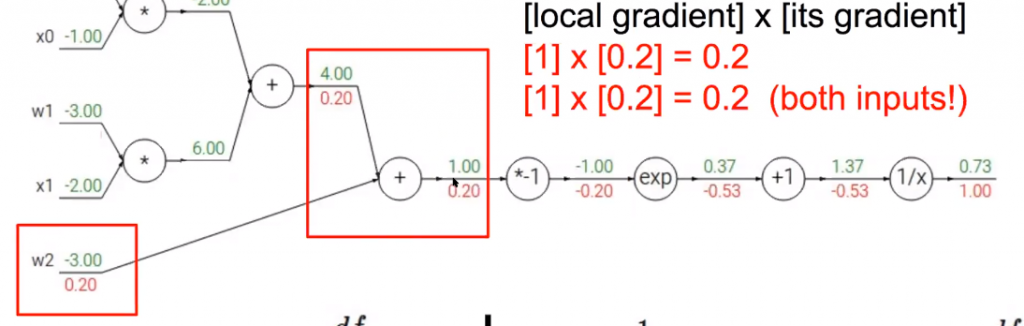
For the cell that has two inputs, we compute both and multiply by the upstream gradient.
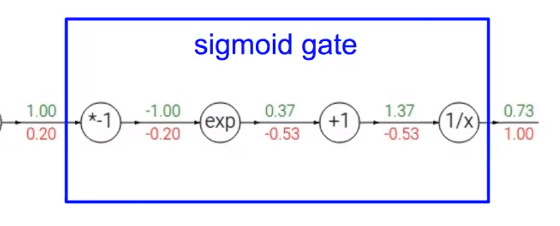
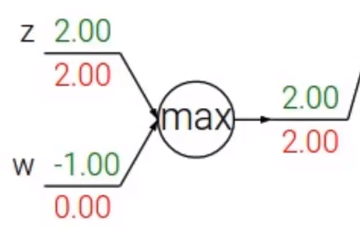
Patterns in backward flow
Add gate: gradient distributor max gate: gradient router mul gate: gradient "switcher" (just like d1=x, d2=y)
sigmoid function:
$$\frac{d \sigma(x)}{d x}=\frac{e^{-x}}{\left(1+e^{-x}\right)^{2}}=\left(\frac{1+e^{-x}-1}{1+e^{-x}}\right)\left(\frac{1}{1+e^{-x}}\right)=(1-\sigma(x)) \sigma(x)$$